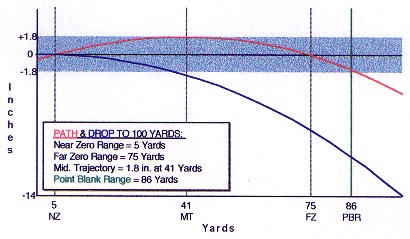
In order to make certain we are all speaking the same language, some definitions of terms are in order. That will be made easier by referring to a chart of the flight of a roundball, generated by a ballistics program, Gun Controller® by Recreational Software, Inc. (RSI).

Line of Sight: A perfectly straight line from the shooter's eye through the rear sight, then the front sight, then the target. On the chart, Line of Sight starts at "0" and is the black line running straight across the chart in the center of the blue shaded area. Obviously, when the shooter aims the gun, he is looking along the Line of Sight.
Line of Bore: A straight line running along the center of the bore of the gun. As we will see, this does not coincide with the Line of Sight.
True Drop: Illustrated as the blue line on the chart, true drop is the actual distance the bullet falls during the time of flight to the target. It is important to realize that this is not the same as what we speak of when we discuss drop in the ordinary sense, which is more properly termed Effective or Apparent Drop. A simple way to think of this is as follows: hold in your hand a roundball perfectly identical to the one being shot , at exactly the same level above the ground; make the Line of Bore of the gun exactly parallel to the earth; fire the gun, and at the exact instant the ball clears the muzzle, drop the ball from your hand. The ball fired from the gun and the one dropped from your hand will both strike the ground at the same instant, one at your feet and the other many yards down range. Since two identical balls, dropped from the same hight, hit the ground at the same instant, they must be dropping at the same rate. That's true because both balls, like everything else on earth, are subject to the acceleration of gravity, which is constant under all circumstances. Regardless of what we do, the ball is 'falling' all the time it is in flight, even when it is traveling upward.
Path: The red line on the chart shows the one thing we are vitally interested in, the actual path through the air of the bullet after it leaves the muzzle of the gun. Many factors effect the final shape of that path, some of which we will discuss.
It is the fact that True Drop is constant and inescapable that everything else in basic ballistics revolves around. To illustrate this, this chart was prepared using a .600 round ball traveling at 1247 ft./sec. The ball weighs 324.3 grains, the gun is sighted in at 75 yards, and the shooting was done under standard atmospheric conditions at sea level (temperature 59F, barometric pressure 29.53 inches of mercury, relative humidity 78%). The chart represents only a hypothetical situation.
The data used to create the chart show that True Drop at 75 yards is 7.55 inches. This means that if we point the barrel, the Line of Bore, directly at the target, the ball will strike 7.55 inches low. Every time, and we can't change that. So, we cheat, in a very simple way. We aim the barrel above the target just enough to cancel out that 7.55 inches of drop. We then adjust the sights of the gun so that the Line of Sight points directly at the target, and we forget it. Now it is easy to see the difference between True Drop and Apparent Drop...We know the ball is actually falling 7.55 inches, but since it hits the target when we aim at it, Apparent Drop is zero at the target range.

Several things follow from this setup. We know that the Line of Bore is below the Line of Sight at the muzzle, because the sights are on top of the barrel. (On the average muzzleloader, that distance is 0.85 inches.) Since the Line of Bore, the barrel, is pointed upward in order to "lob" the ball in on the target, the Line of Bore must cross the Line of Sight, going upward. The ball, which starts out along the Line of Bore, quickly falls below it, but not before it has crossed the Line of Sight. Depending upon the gun, the velocity and the range the gun is sighted for, this happens at 5 to 10 yards in front of the muzzle. Where the bullet crosses the Line of Sight the first time, going upward, is called the Near Zero Range, NZ on the chart. The bullet travels on, reaching its maximum height above the Line of Sight, then begins to fall. The point at which this maximum above Line of Sight is reached is called Mid-Range Trajectory, MRT on the chart. This occurs, in general, at a lottle more than 50 percent of the distance to the target. Continuing on, the bullet falls closer to the Line of Sight, until it crosses it again at the target range, the Far Zero Range.
We now have the picture of the Path from muzzle to target...below the Line of Sight at the muzzle, crosses the Line of Sight close to the muzzle at the Near Zero, reaches a maximum height above the Line of Sight at the Mid-Range Trajectory, stays above the Line of Sight until it crosses it again at the target range, Far Zero.
In considering external ballistics at our very basic level of discussion, one more facet of the problem needs to be discussed, that of the shape of that pretty red line on the chart. The perfect Path would coincide exactly with the Line of Sight, and to see the target would be to hit it. Sorry, won't ever happen. Obviously, different bullets, fired at different velocities, will perform differently. A major factor in determining the shape of the Path is the rate at which the bullet, of whatever shape, slows down. Since True Drop is a constant, occurring at a constantly accelerating rate, we can see that if a bullet is traveling very fast, it will travel a long distance downrange for any given unit of time, and for a certain amount of True Drop. If it is traveling slowly, it will travel a much shorter distance downrange in that same unit of time, but it will drop exactly the same amount. Thus, the shape of the Path is fairly flat at the beginning, but curves more and more as it nears the target, because the bullet is slowing down. The shape of all trajectories is similar to that of a parabola, with constantly increasing rate of curvature.
Why does one bullet slow down more quickly than another? Simply put, because it has more drag (more friction through the air), or less inertia. Why does one have more drag? Because of a difference in shape which creates more friction. A streamlined bullet cuts the air more easily than a blunt, irregularly shaped one. So, a bullet designed for and fired from a modern, high velocity rifle will have much less drag than a conical or a roundball fired from a black powder gun. Inertia is the property that makes any moving body tend to keep moving in the same direction and at the same speed, unless acted upon by some outside force. Inertia is increased by increasing mass (think weight) and velocity. Our flying bullet is acted upon by two outside forces, gravity forcing it to drop and air friction forcing it to slow down.
It becomes obvious, then, that heavier bullets and more streamlined bullets resist slowing best.
In order to be able to compare the efficiency of various bullets, a mathematical tool was developed, and it's called the Ballistic Coefficient (BC). Only a mathematician could love it, but it's really quite simple. A bullet of a given shape (the shape doesn't matter) and weight was fired thousands of times, and its drag, its rate of slowing, was determined precisely. This was named the Standard Bullet. Now in order to compare the performance of our favorite projectile, all we have to do is compare its rate of slowing with that of the Standard Bullet. If it slows exactly the same as the Standard bullet, it is said to have a Ballistics Coefficient of 1.0. Any BC lower than 1.0 indicates a bullet which is not as good at plowing through the air and retaining its velocity as the Standard Bullet is. Those of us interested in black powder shooting and the ballistics of our bullets quickly learn that the BC of a roundball is lower than that of a conical, and that both are much lower than the Standard Bullet. Because a roundball is....a round ball...., its shape cannot be changed. To compensate for a low BC, we can do two things, increase the weight, because a heavier projectile has more inertia and resists slowing more, and start with greater initial velocity, so that velocity at the target is higher, even after all the loss.
Tomes have been written about external ballistics, and this discussion has barely scratched the surface. Still, if you paid close attention, there's no reason your targets should not look like this.

©1997 B.E. Spencer